Intuition - Quadratic Formula
Last class, we learned about the quadratic formula and the discriminant (I am talking about math!).
The Quadratic Formula
This is basically completing the square, but with more manipulations.
If you remember from Intuition: Completing the Square, what we have so far is: \((x + \frac{b}{2})^2 - \frac{b^2}{4} + c = 0\).
If you add back \(a\) in the quadratic, you find that it barely changes the equation into:
\((x + \frac{b}{2a})^2 - \frac{b^2}{4a^2} + c = 0\).
If you rearrange this (I’ll leave this to the viewer), you eventually get:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]That’s the quadratic formula.
The Discriminant (I’m talking about math!)
You might wonder what restrictions there are in the quadratic formula. An obvious one is that \(a \neq 0\) because you would divide by 0. This, in the quadratic, basically means that the quadratic term can’t be 0. This makes sense because then it wouldn’t be a quadratic equation, it would be a linear equation. But another one is the square root. If \(b^2 - 4ac < 0\), then the square root will be rooting a negative, which (for our purposes now) will give an error.
Another thing that you may notice is that the square root is being \(\pm\)ed. This means that if \(b^2 - 4ac = 0\), there is only one solution, because it would be \(\pm 0\), which doesn’t affect anything.
This term, \(b^2 - 4ac\), seems to determine a lot of things, so math people gave it a name: the discriminant (I’m talking about math!). We might as well list out all of the cases.
If \(b^2-4ac > 0\):
There are two real solutions.
If \(b^2-4ac = 0\):
There is one real solution.
If \(b^2-4ac < 0\):
There are no real solutions (and two imaginary solutions, but that doesn’t matter for our purposes now)
In fact, this also has some meaning on a graph. But first, we need to figure out how to graph this.
We should probably make \(x\) our independent variable, because we can plug anything into it. Then the result would be \(y\). Finally, the roots to the equation would be where \(y = 0\). This means we can finally graph the quadratic equations.
Here’s for \(b^2-4ac > 0\):
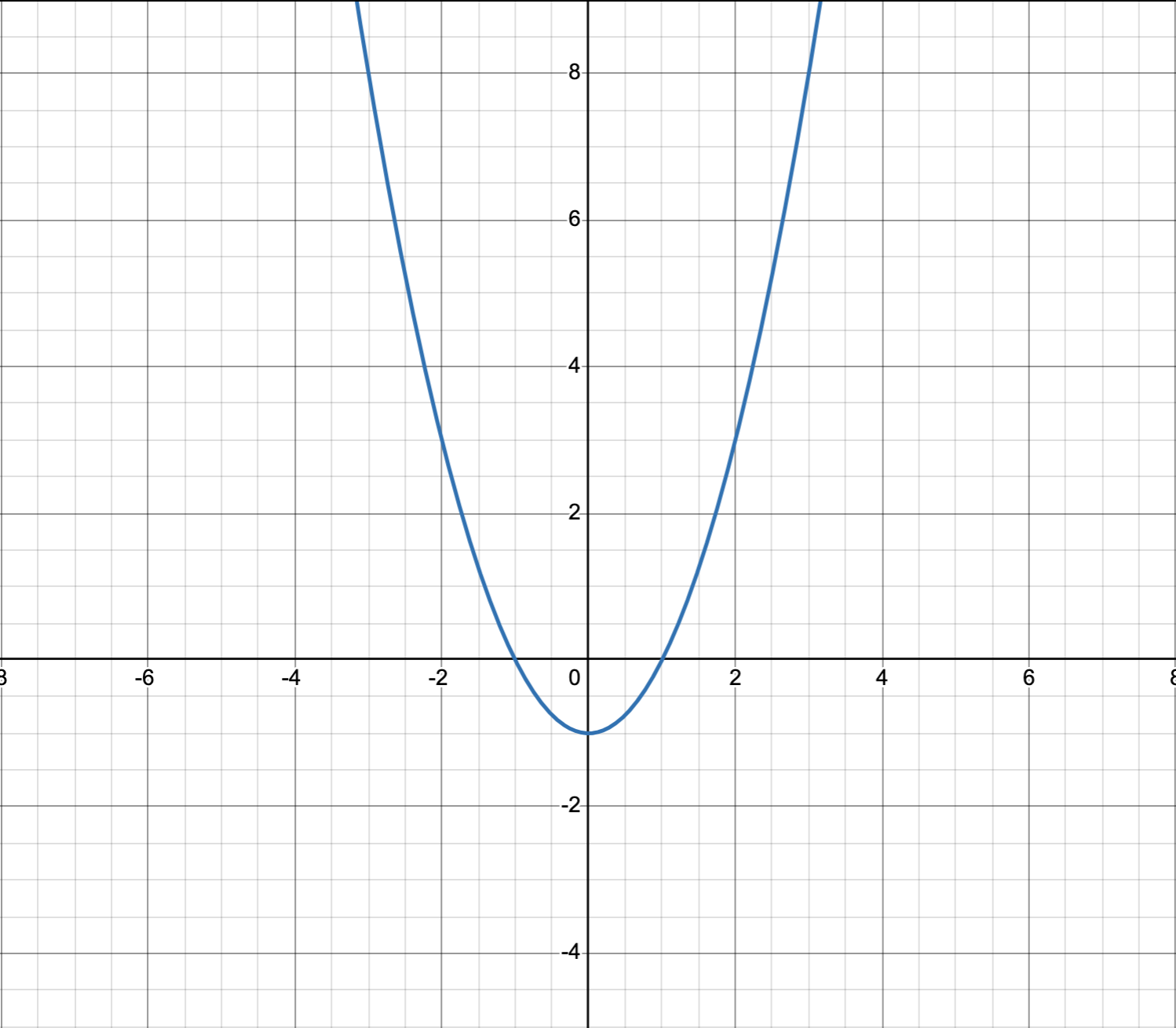
Here’s for \(b^2-4ac = 0\):
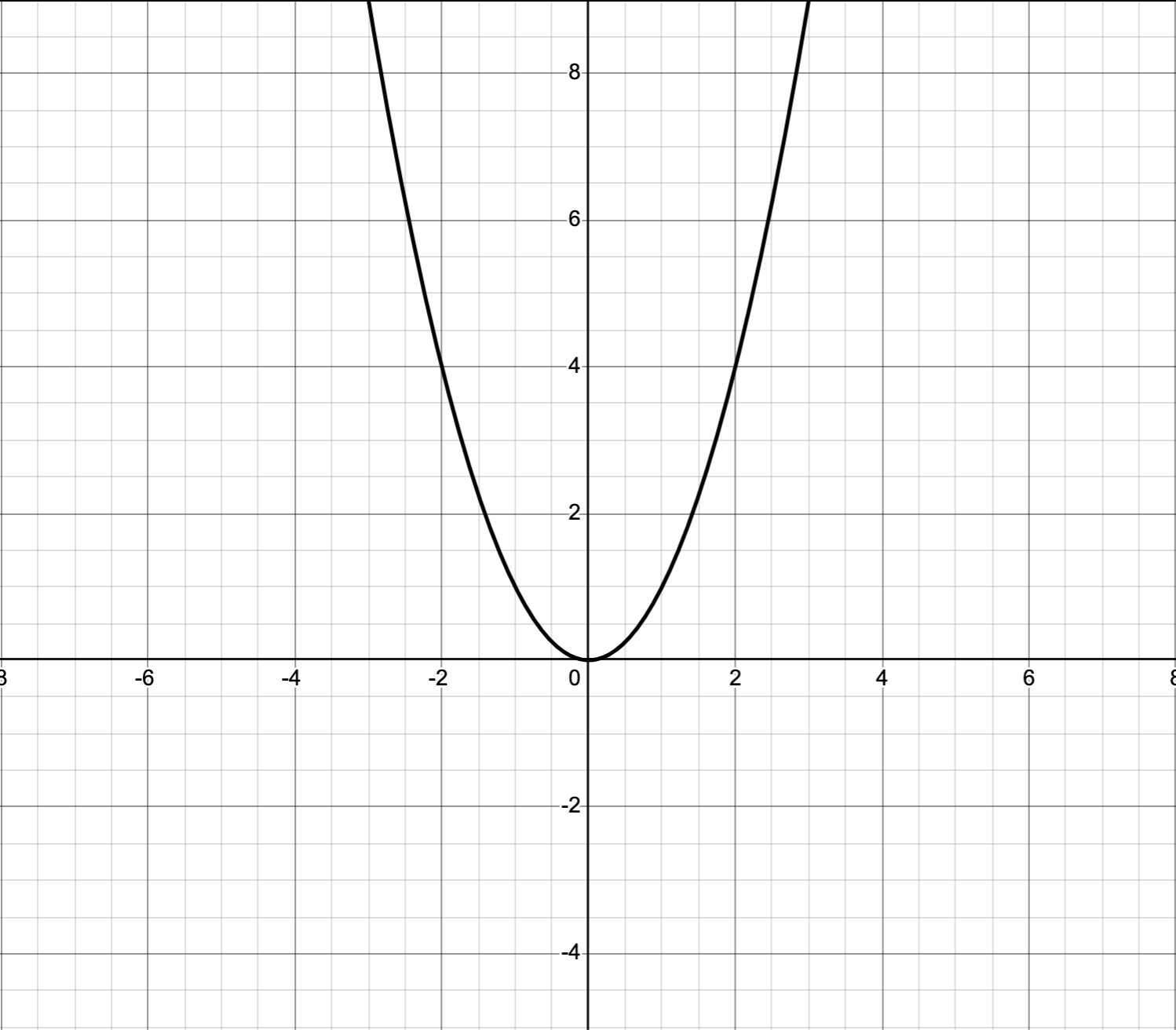
Here’s for \(b^2-4ac < 0\):
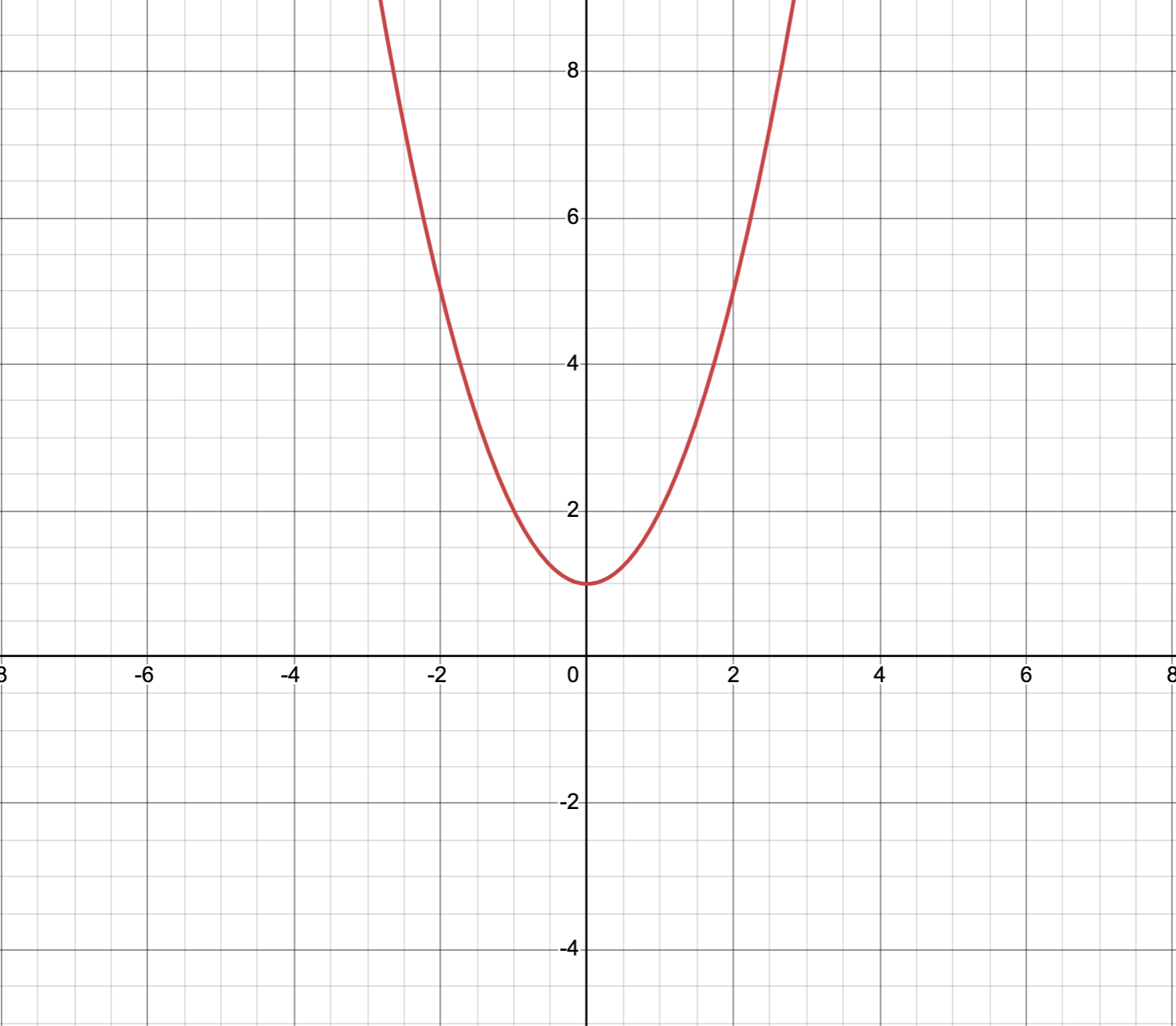
Conclusion
The quadratic formula is not a very complex extension of completing the square, but it is still very useful and can lead to other insights involving quadratics too. I am still not done with quadratics: there are still many things we are going to learn.