Intuition - Trig Functions
Today, we learned the basic trig functions. This is actually part of the radicals unit. If you are wondering why there hasn’t been many posts lately, it’s because I wanted to do all of radicals in one post.
What is Trigonometry
Trigonometry, or trig for short, relates angles in a right triangle to the sides.
It should be intuitively obvious that any right triangle with legs \(a\) and \(b\) are the same. That must mean that the angles in the right triangle are also the same, so we can create a few functions that relate the angles to the sides because both of those values are unique to each other.
Basic functions
There are three basic functions: sine, cosine, and tangent. They are usually abbreviated as sin, cos, and tan, respectively.
These three functions take in an angle as an input and spit out a ratio as an output. Usually, they are described with the mnemonic “soh-cah-toa”. To understand this, let’s look at an actual right triangle.
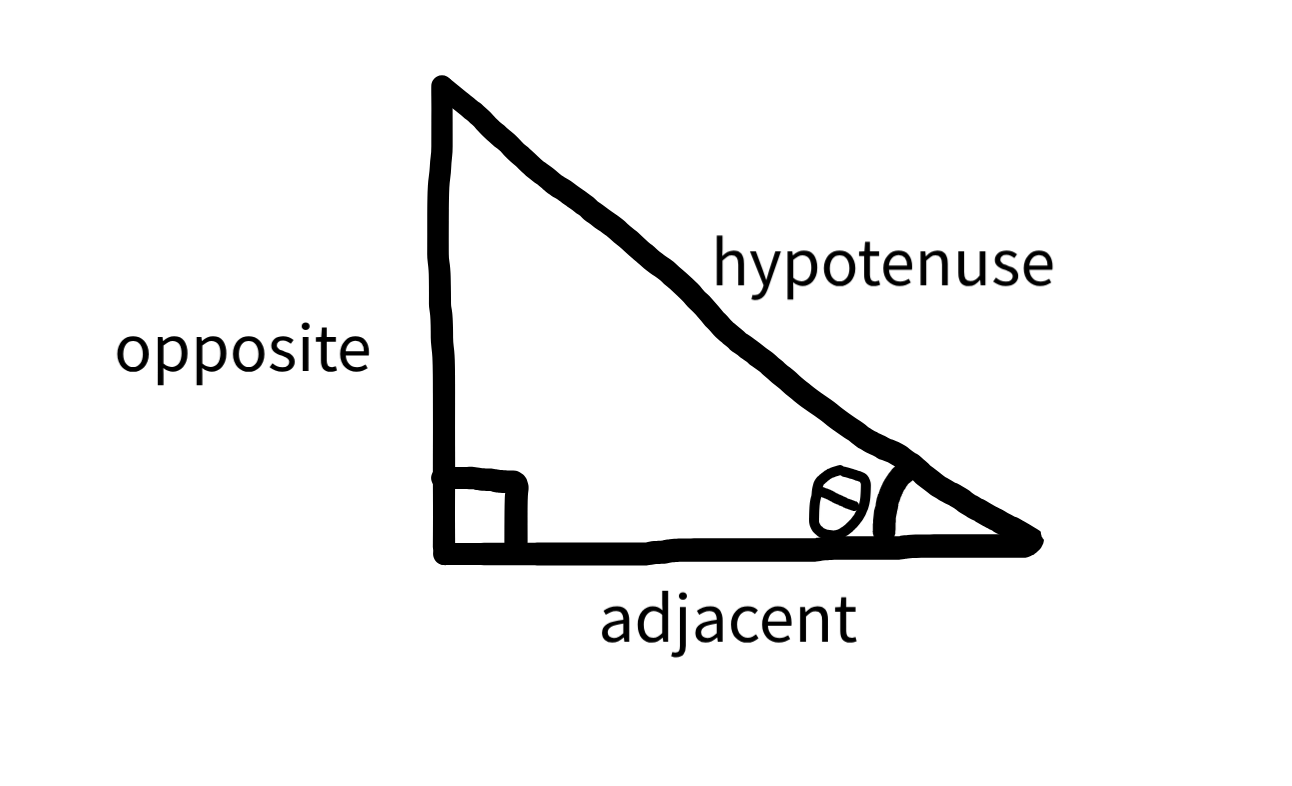
Here I have labeled some of the sides. Now we can understand “soh-cah-toa”. The first part of it is “soh”, which means \(sin(\theta) = \frac{opposite}{hypotenuse}\). Following the same rules, we find that the next parts mean \(cos(\theta) = \frac{adjacent}{hypotenuse}\) and \(tan(\theta) = \frac{opposite}{adjacent}\).
I think a better way to remember this is to think of sine as (kind of) the y-coordinate, cosine as (kind of) the x-coordinate, and tangent as (kind of) the slope.
The reason for the “(kind of)” is because sine doesn’t exatly equal the y-coordinate, sine * hypotenuse equals the y-coordinate. The reason for this is also based on intuition.
In the section before, we found that any right triangle with the same legs is the same. An intuitive addition to this is that when you scale a right triangle, the angles stay the same. This means that \(sin(\theta)\) isn’t always the y-coordinate, since if you scale it, \(\theta\) is the same, but the height of the triangle is different. This means that \(sin(\theta)\) has to multiplied by a scaling factor, and a logical scaling factor would be the hypotenuse. This is logical because sine, cosine, and tangent don’t touch the hypotenuse at all. We also need a base scale for \(sin(\theta)\), and it makes sense to set this as 1.
All of this means that \(sin(\theta) * hypotenuse = y\hspace{0.1cm}coordinate\). Cosine also works this way, but for the x coordinate instead.
Tangent, on the other hand, is \(\frac{sin(\theta)}{cos(\theta)}\). If you multiply the top and bottom by the hypotenuse, you get that \(tan(\theta) = \frac{y\hspace{0.1cm}coordinate}{x\hspace{0.1cm}coordinate}\), which is also the slope of the line.
Solving Problems
In some problems, it will ask you to find the length of a side given another side and an angle or to find an angle given two side lengths.
To solve these types of problems, you can write an equation containing one of the trig functions. Whichever two sides your problem relates to, you can find the trig function that contains both of them.
If you have to find the angle, you might need an inverse function. Just like subtracting is adding’s inverse or dividing is multiplying’s inverse, an inverse function is said function’s undoing move.
Basically, you will have this type of equation: \(f(\theta) = a/b\).
Then, you take the \(f^{-1}\) of both sides to get this: \(f^{-1}(f(theta)) = f^{-1}(a/b)\). By definition, \(f^{-1}(f(x)) = x\) (basically undoing the function), so \(\theta = f^{-1}(a/b)\).
Conclusion
These trigonometric functions are only the start. There are many other identities, like the half angle identity or the sum to product identities. Those identities are when trig gets really interesting. I probably won’t get to any of those soon, but you can learn them on your own with maybe a textbook.