Intuition - Factoring Part 4
These past 3 classes, we didn’t do much except for review and take quizzes.
We learned: Solving non-linear equations, finding x-intercepts and y-intercepts of a quadratic graph, finding the vertex of a quadratic graph, and factoring sum and difference of cubes.
Solving Non-Linear Equations
This might seem like a completely new concept, but it’s actually pretty simple to do if you know how to factor.
First, you isolate all of the terms on one side. That means that the other side will be \(0\).
If you factor something, you have a bunch of terms on one side, all multiplied together. Because all of these terms multiplied together equals \(0\), one of the terms must equal \(0\).
From there, you can use casework on each term to see what x would have to be if that term is \(0\). Once you repeat for each term, you have all of the possible solutions.
Finding Stuff on a Quadratic Graph
The graph equation looks like this: \(y =\) quadratic.
Finding x-intercepts
To find the x-intercepts, we need to find points such that \(y = 0\).
If we plug this into the equation, we see that we need to find \(x\) where \(0 =\) quadratic. We already know how to do that, we just solve the quadratic.
Finding the vertex
Generally, a quadratic equation looks something like this (it might be lower and have 2 intersections, higher and have 0 intersections, or be upside down):
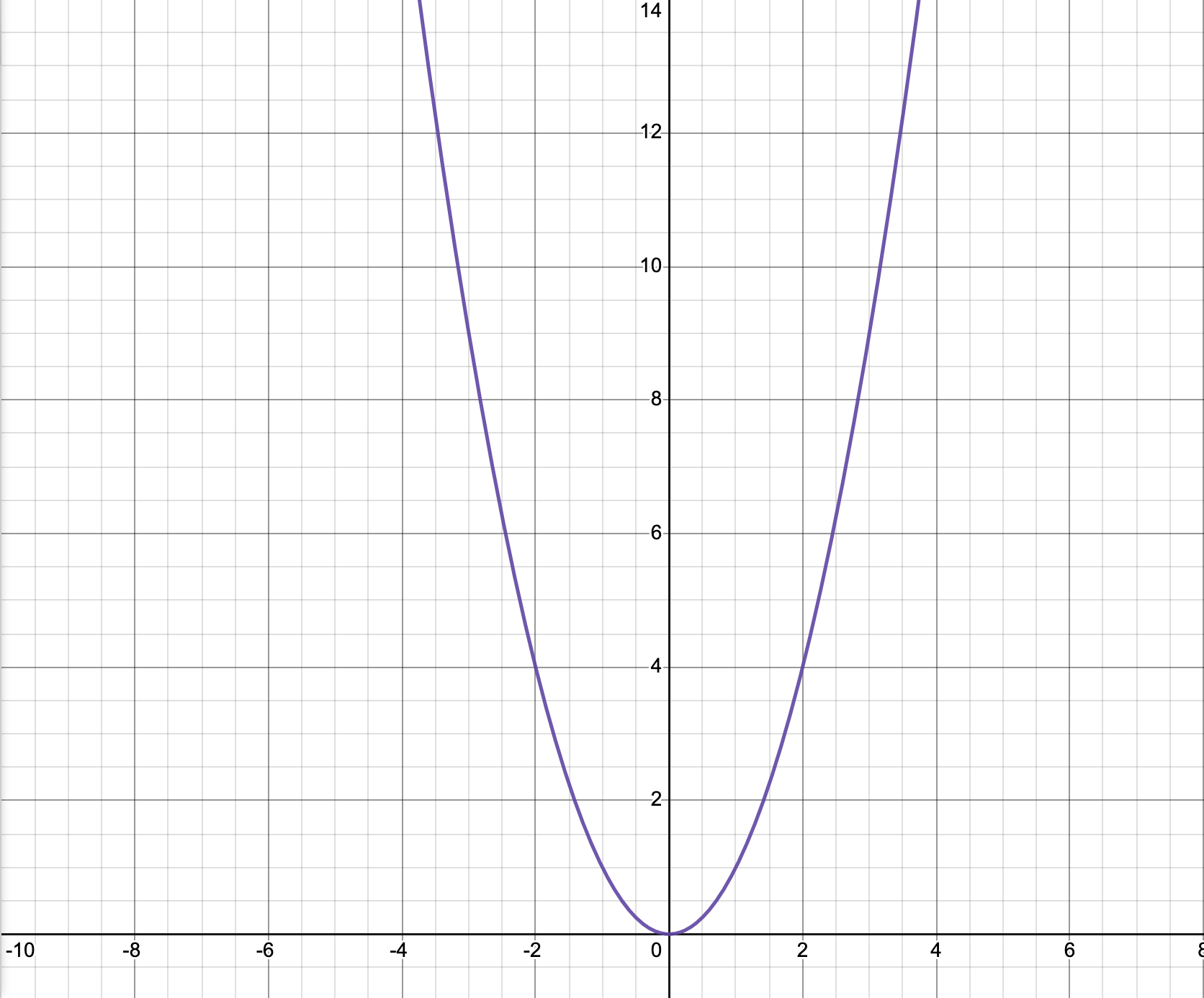
The vertex is the place where the quadratic starts to go the other way.
One thing you may notice about quadratics is that they are symmetrical about the y-axis. It makes sense that the vertex is on the line of symmetry if you look at the image, so the x-coordinate will be the average of the roots, or \(\frac{r + s}{2}\).
I don’t know if I mentioned this before, but the sum of the roots is \(\frac{-b}{a}\). This is because the expansion of \((x-r)(x-s)\) is \((x^2 - (r + s)x + rs)\), so \(b\) is \(-(r+s)\). If \(a\) isn’t \(0\), this rule still works.
We can see that the average of the roots has the sum of roots in it, so we can substitute our expression in: \(\frac{r+s}{2} = \frac{\frac{-b}{a}}{2} = \frac{-b}{2a}\).
Then, we can plug this in to find the y-coordinate.
Factoring Sum and Difference of Cubes
I already covered this in Intuition: Multiplying Polynomials.
Conclusion
Sorry for not posting for 3 classes, but we didn’t do much learning, so I decided to not post until now.
I don’t know what we’ll be doing for the rest of this unit or what the next unit to be, but definitely stay around for completing the square and the quadratic formula.