Intuition: Factoring Part 3
Today, we learned another way of factoring when \(a\) isn’t \(1\). We also learned how to identify and factor perfect squares.
Also, I forgot about a very intuitive way to distribute 2 binomials, so I’ll include that here.
Another Way of Factoring When \(a\) Isn’t \(1\)
It turns out, last class, we only learned how to do this when you could factor \(a\) out perfectly.
The concepts that we learned this class are guess and check and factoring by grouping. We already covered guess and check in my previous intuition series post: Intuition: Factoring Part 2
Grouping
Say we have a polynomial: \(ax^2 + bx + c\)
We need to find \(2\) factors of \(ac\) that add up to \(b\). Then, you can split \(b\) up into those factors, and then you have a 4-termed polynomial. That means that you can factor it by grouping.
This becomes \(ax^2 + b_1x + b_2x + c\). When we group \(ax^2\) with \(b_1x\), it doesn’t always work out. If it doesn’t work out, then group \(ax^2\) and \(b_2\).
Why does this work?
Basically, a mathematical coincidence.
Let’s look at the expansion of \((dx + f)(gx + h)\) again. This expands to \(dgx^2 + fgx + dhx + fh\). When we multiply \(a\) and \(c\) together, we get is \(dgfh\). When we multiply the two terms of the linear coefficient, we also get \(dgfh\). That means that we just have to guess and check until we find those two factors that work. Then, factoring should be easy with the grouping method.
How to Factor Perfect Squares
To factor something, we need to figure out how to distribute it.
This is the distribution:
\((ax+b)^2 = a^2x^2 + 2abx + b^2\).
That means that if you see something resembling that, you can factor it into a perfect square.
Important Intuition for Distribution
Distribution is just distributing, but one thing I missed is a image that gains a lot of intuition. This image is also very important for completing the square.
This shows the distribution for \((ax + c)(bx + d)\), because the result is the same as the area of a rectangle that has side lengths of \(ax + c\) and \(bx + d\).
Here’s the image:
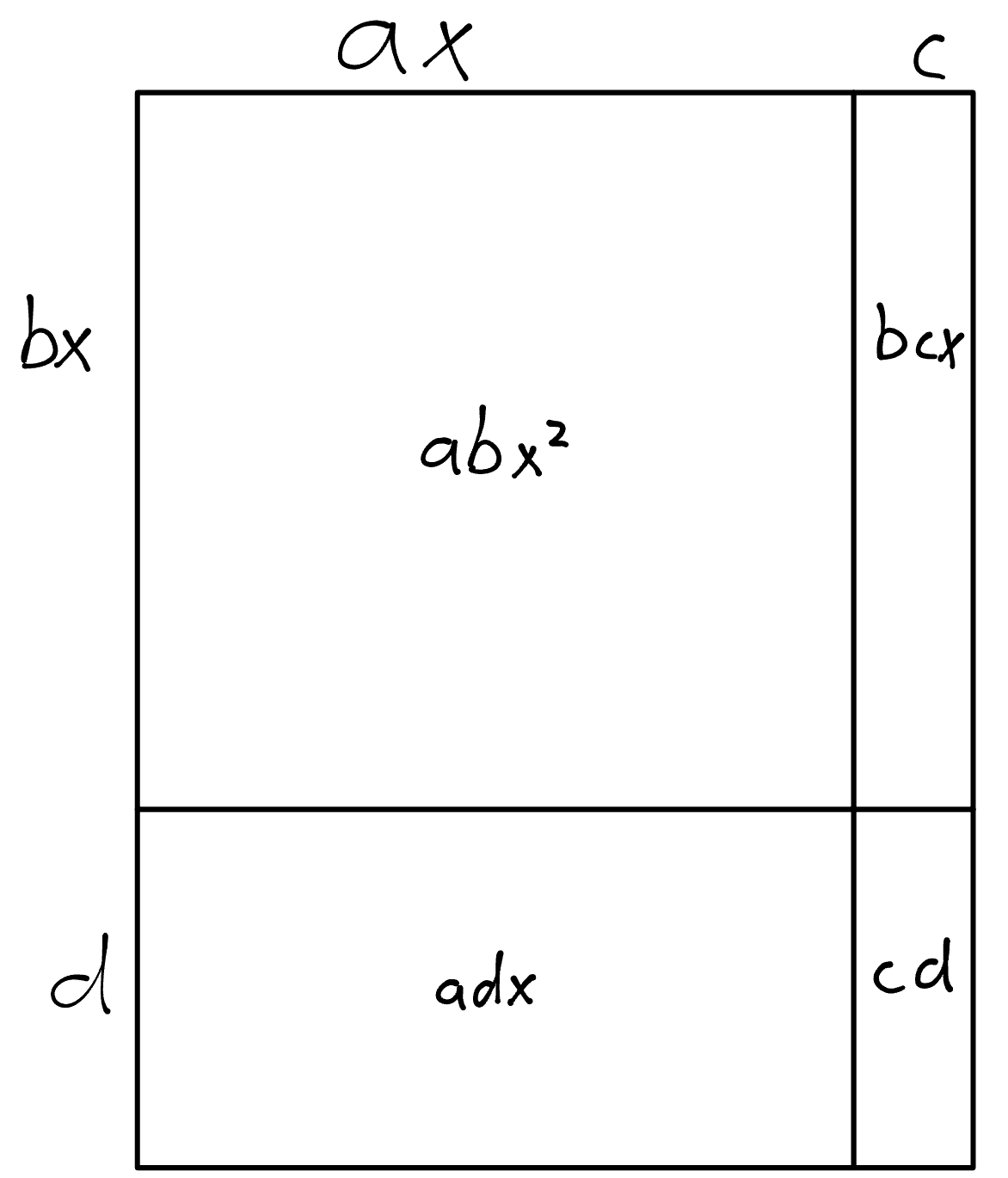
If you have more binomials, you expand it into higher dimensions, and if you have trinomials or polynomials, just make more sections on the side.
Conclusion
I learned that we aren’t going to do completing the square or the quadratic formula in this unit, but we are going to be doing this year, after the radicals unit. Stick around for that - completing the square has a really nice intuition visualiziation.