I Found Primes
Recently, I was thinking about finding a prime-finding algorithm. This eventually led to me basically rediscovering the Sieve of Eratosthenes algorithm.
The Start
I was thinking about the sorting algorithm, “sleep sort”. This is a horrible sorting algorithm. Basically, to sort a list, the computer assigns a function to each number that says, “say (number) after (number) seconds”. Then, we can track what the computer says, and the order of numbers that comes out will be our sorted list.
Just After the Start
One of the easiest algorithms to understand is what I would call the “mod algortithm.” This uses the fact that prime numbers don’t have any divisors other than 1. An easy way to test this would be to see if n mod p = 0, if n is the current number we’re checking and p is the prime. If n passes all of the tests, we add it to a prime list and can start using it as a value for p now. We can keep on doing this for however long we want.
The problem with this is that the mod algorithm is very slow. Not only is the mod function very slow, the number of mod functions you need to do increases with \(n^2log(n)\) if n is the prime that you are searching to (I think). Even with various optimizations, this number will still grow.
What does this have to do with my prime algorithm? Well, I wanted to do the same thing, but just without the mod function, and hopefully with a better time complexity.
I realized that you can imitate the mod function by sending an update every n numbers, starting with an update at t = 0. If the update is there, that means that it is a multiple of n, meaning that the mod function of n is 0. If you want to send an update every n numbers, that sounds kind of like sleep()!
This completely gets rid of the mod function, and also makes it so that we don’t have to check every number lots of times, which brings down the time complexity to linear time.
The problem with this is that sleep() isn’t always perfectly accurate, and that there isn’t an easy way to see if sleep() has ended or not (there’s probably a way to do this, I just don’t know it.)
Because of this, I thought that maybe you could use a list to make the sleep() function. Basically, each list entry has a time until update. Every time the loop updates, I will decrease every entry by one, which is basically the same as 1 second passing.
There’s also a problem with this, though. The amount of primes increases, so the number of entries in the sleep list also increases. This means that the number of updates for the sleep also increases, because I need to change every entry, which is increasing. All of this means that this also is kind of slow.
Eventually, I realized that I could just create a time variable and only update the sleep list if it is a multiple of the number. This would make it so that I didn’t need to update every entry in the sleep list every timestep.
Comparisons
I compared this algorithm with the Sieve of Atkin (which the internet said was really fast) and the mod algorithm. The Sieve of Atkin is green, my algorithm is blue, and the mod algorithm is red.
Here’s a linear to linear graph:
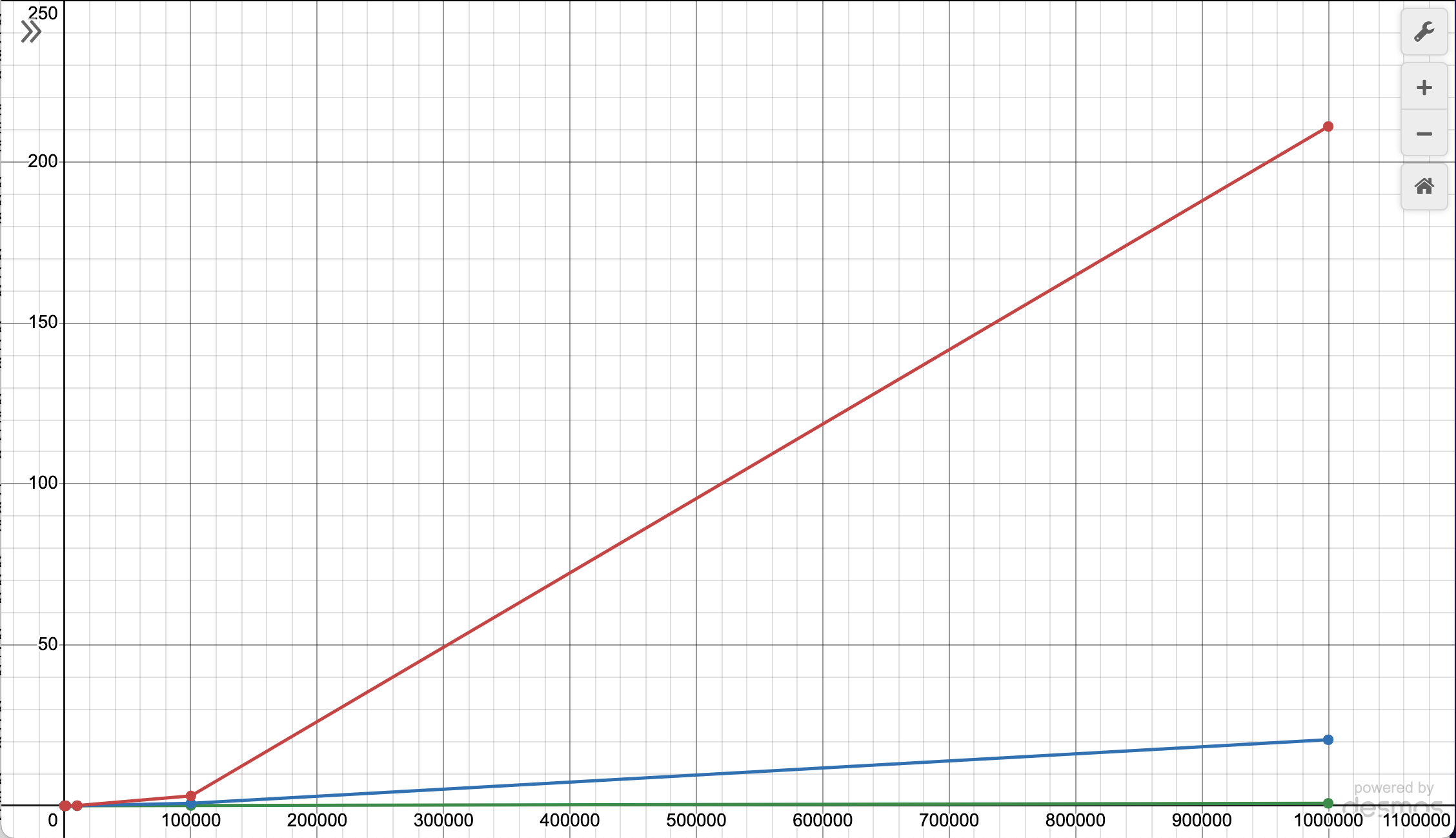
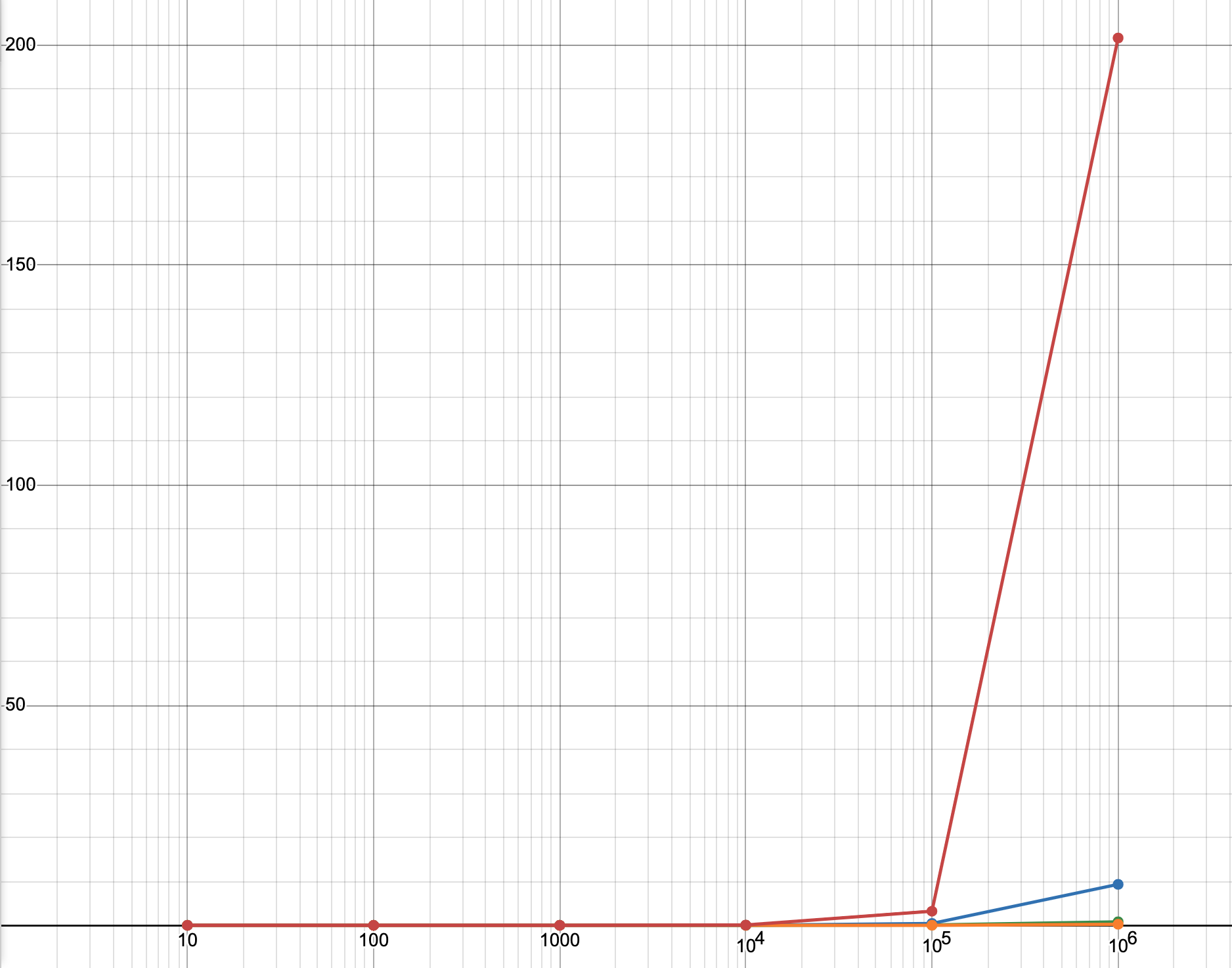
The data points on the left are smooshed together, so here’s a graph with the x-axis in a log scale. This basically squishes the numbers together more as they get larger.
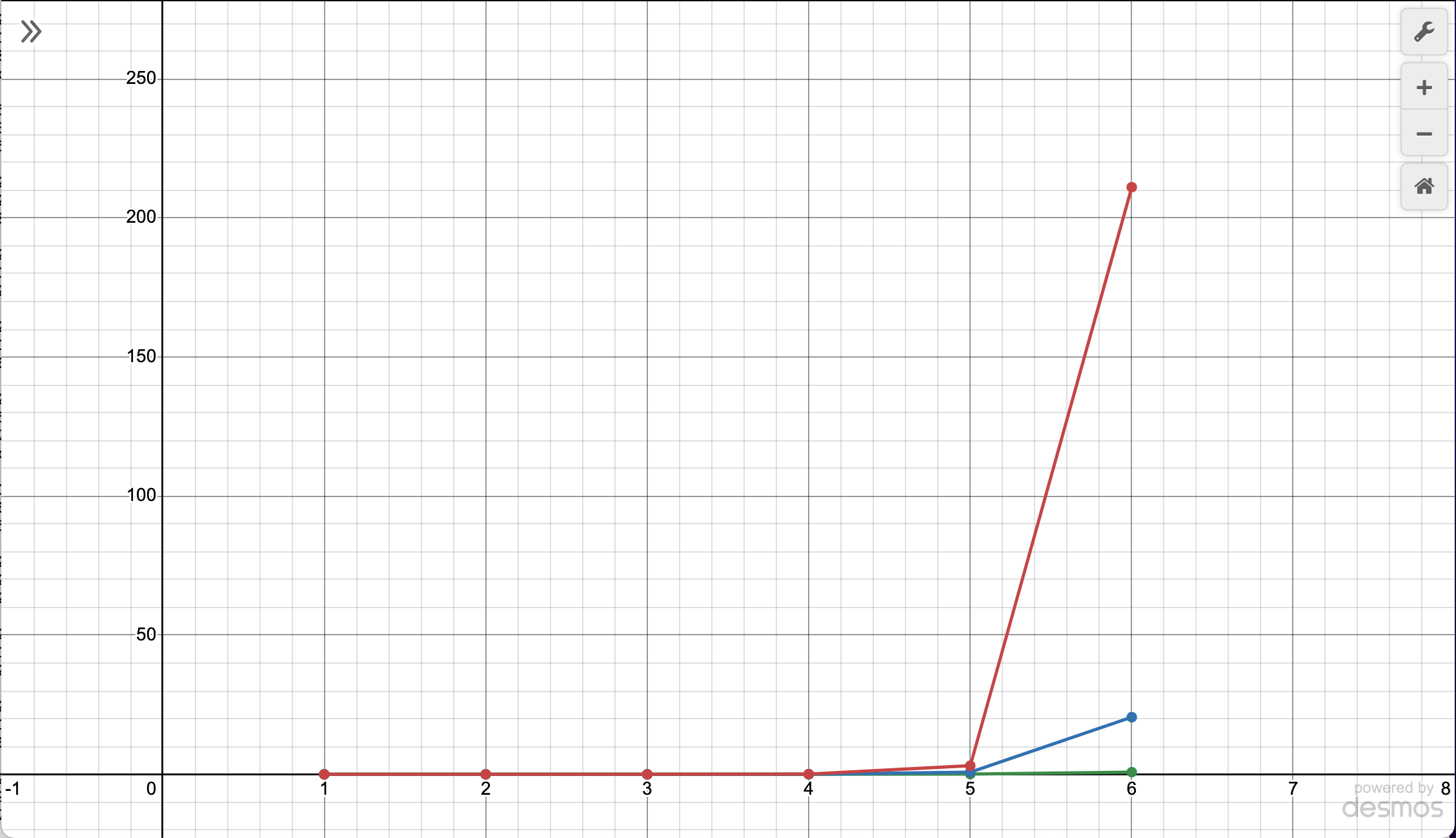
This still doesn’t show the difference between points in the far left, where their difference is masked a lot by the bigger difference on the right. I made the y-axis also a log scale because of this.
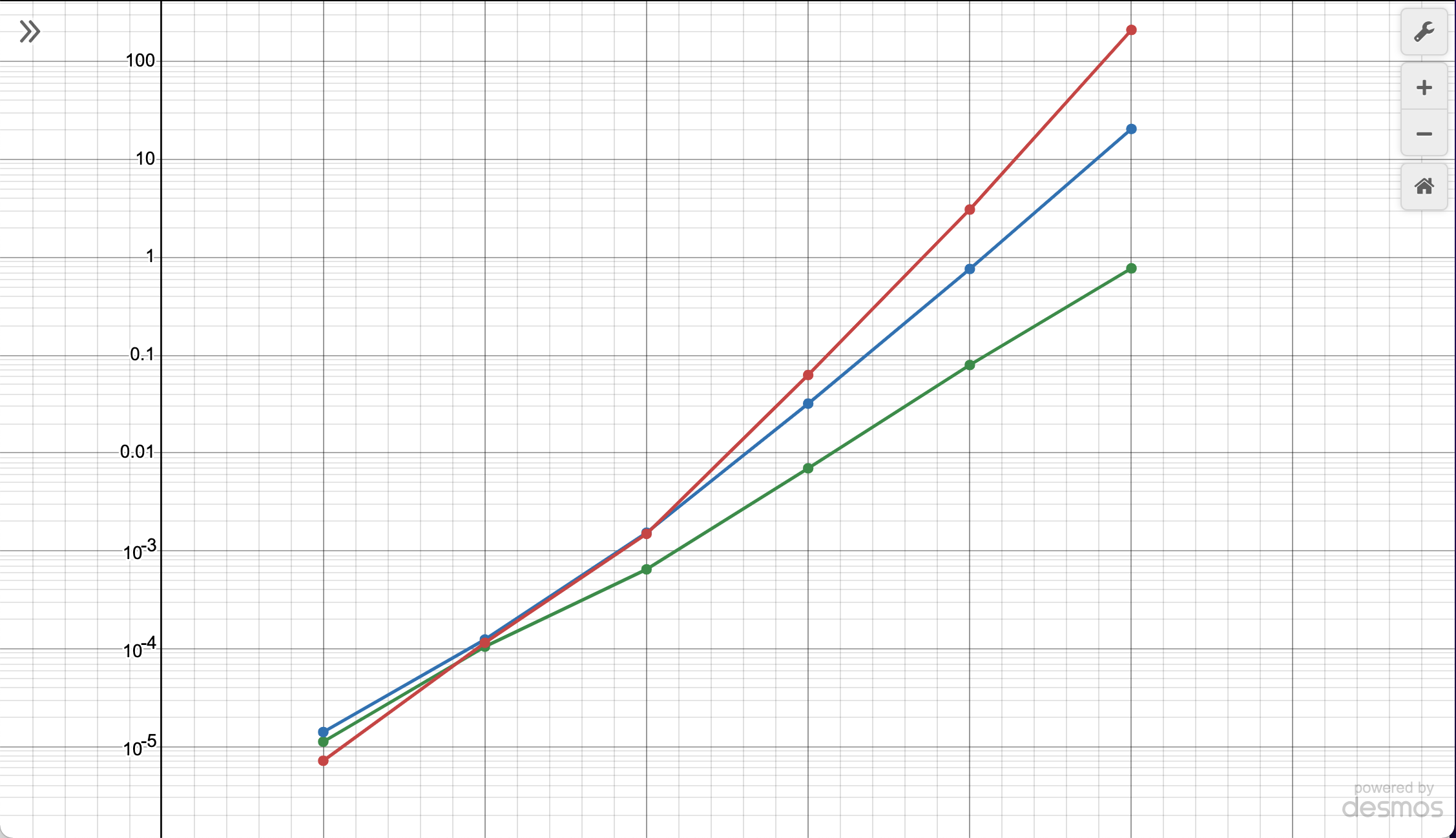
From this, we can see that the mod algorithm grows rapidly. Just a note, on a log scale, there doesn’t seem to be a very big difference, but there actually is. What looks like one unit between the mod algorithm and my algorithm in the end is actually an x10 difference.
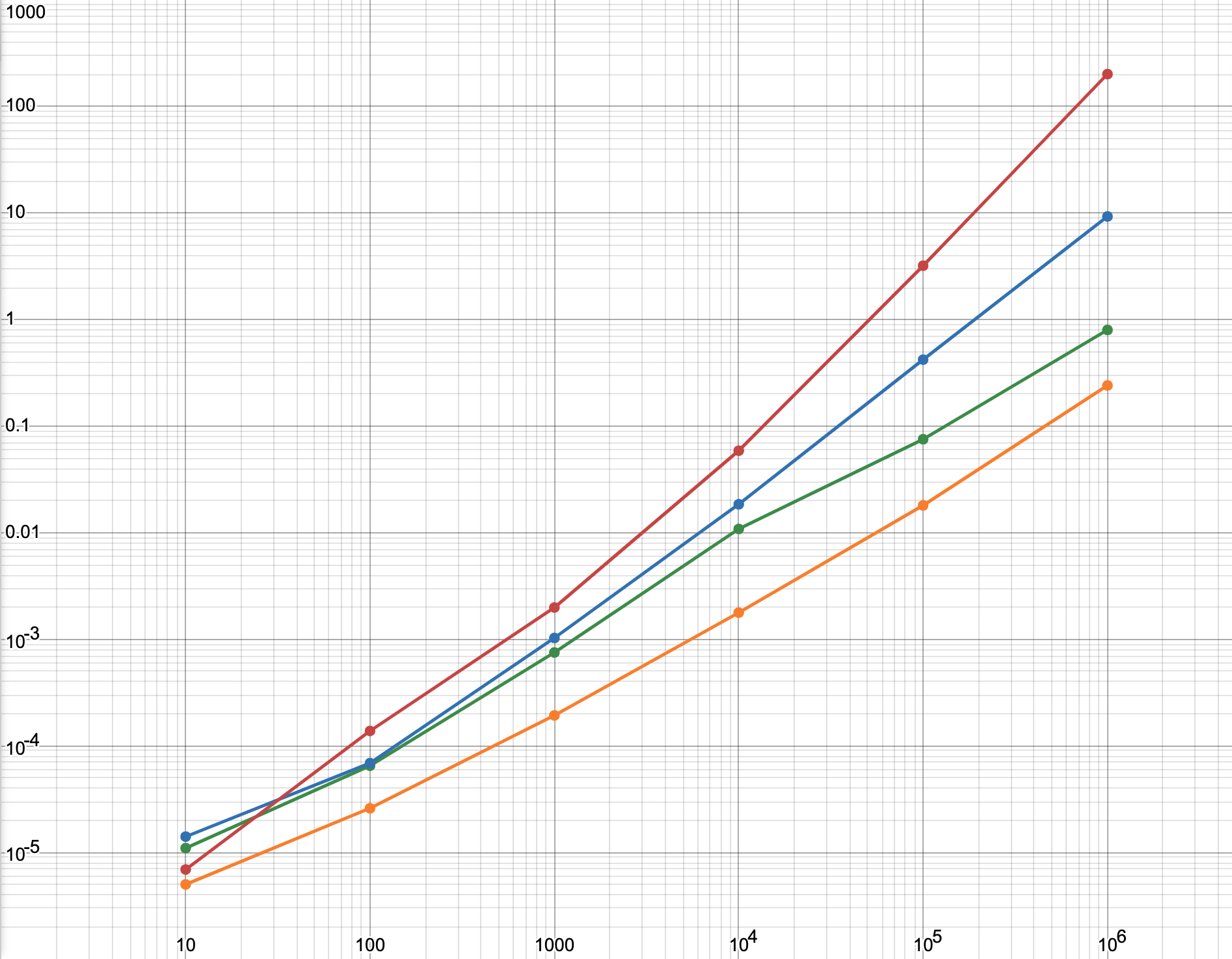
After this, I realized that this is basically the Sieve of Eratosthenes. After implementing some of the optimizations found there, these are the new statistics (Sieve of Eratosthenes is orange):
Linear linear graph:
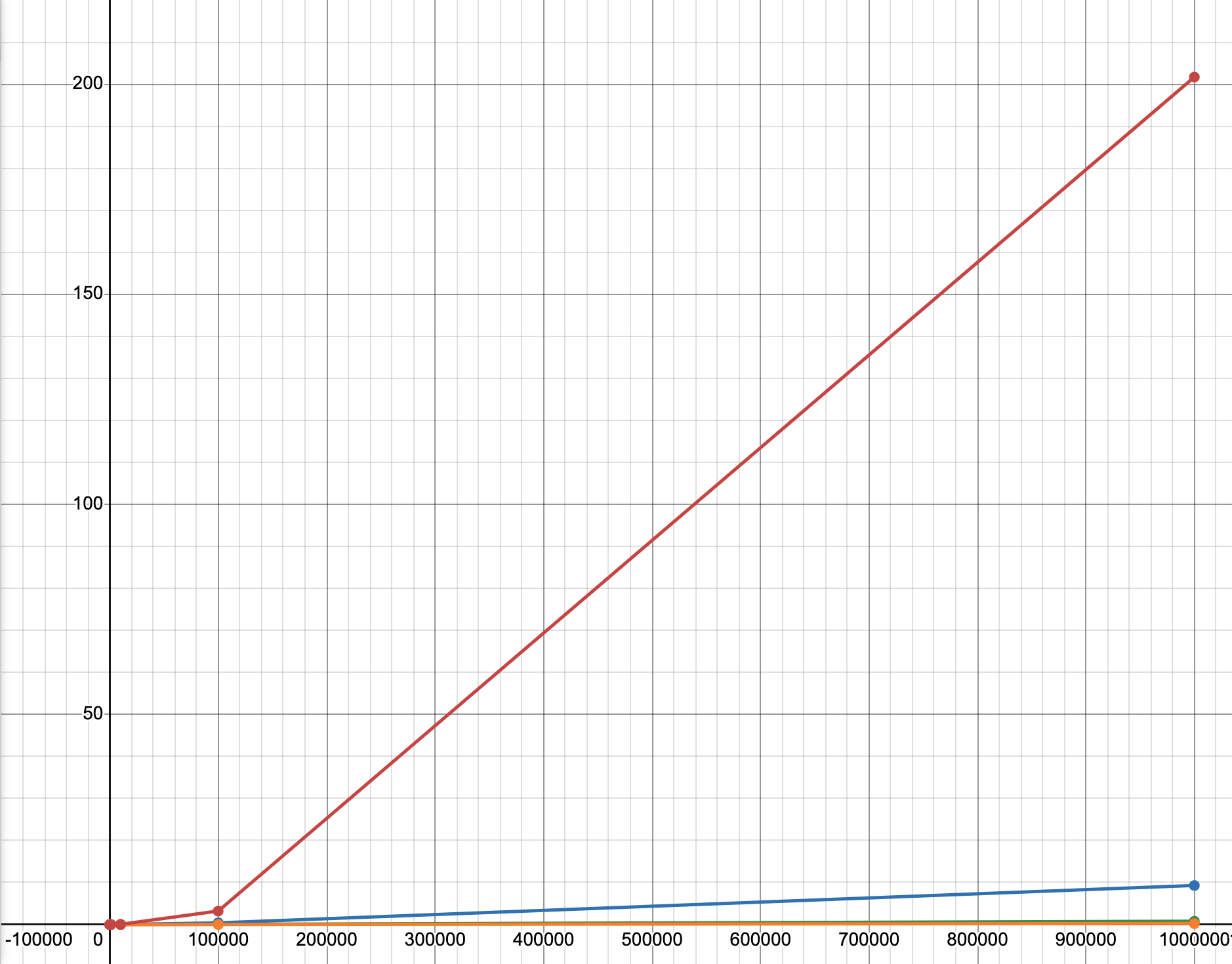
Linear log graph:
Log log graph:
Differences
You might be surprised that the Sieve of Eratosthenes did better than my algorithm, because I said that I basically rediscovered it. I did kind of rediscover it, but I did it in a pretty bad way.
In the Sieve of Eratosthenes, it takes all the multiples and marks them down. In my algorithm, it takes all the multiples and marks them down sequentially.
Basically, the difference is that in the Sieve of Eratosthenes, it takes all of the multiples of the current prime and marks them down, then moves to the next prime, and so on. In my algorithm, it checks every prime for a multiple every timestep. This means that instead of doing one operation per multiple (marking that multiple to be not a prime), I’m checking a lot of numbers for being a multiple, with only some actually being a multiple. In this way, my algorithm is a lot less efficient.
Conclusion
I think prime-finding algorithms are a relatively solved area of math because humans have had a lot of time to figure out this type of stuff.
Still, I appreciate the work put into this type of stuff more now (like try understanding the Sieve of Atkin!)