Does Speed Affect the Amount of Rain on Your Rainshield?

I did get this idea from looking at rain on the windshield.

For now, the angle of the windshield is 45˚. The blue box represents the area of the possible rain that could end up on the windshield in the alotted time. Also, assume the density of the rain is constant.

Now for the speed part. The red area represents the area of rain that will hit the surface, dependent on the speed. Here are the boxes for a speed of 1, 2, and 3.

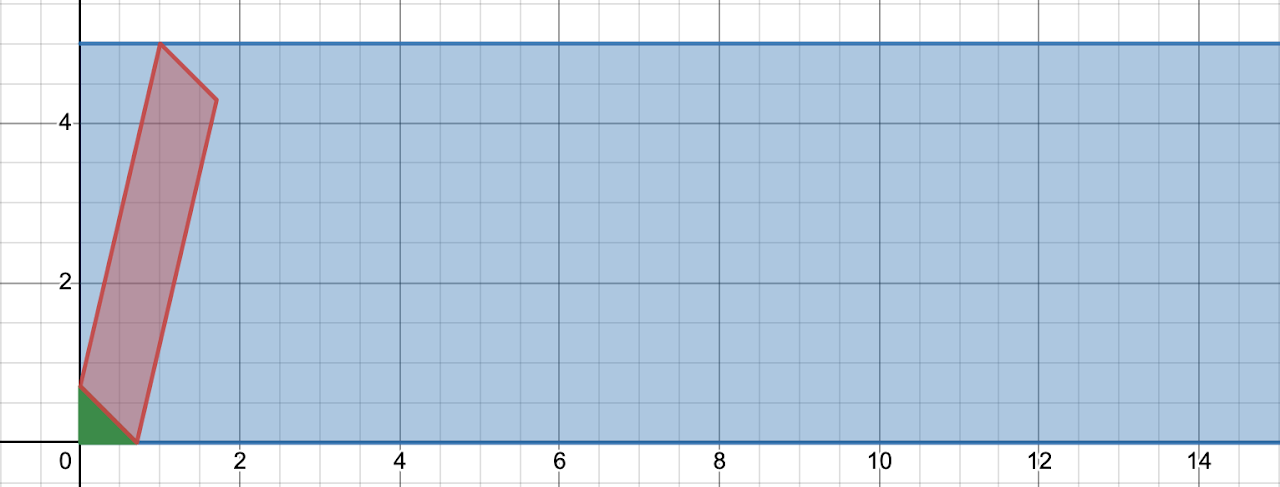
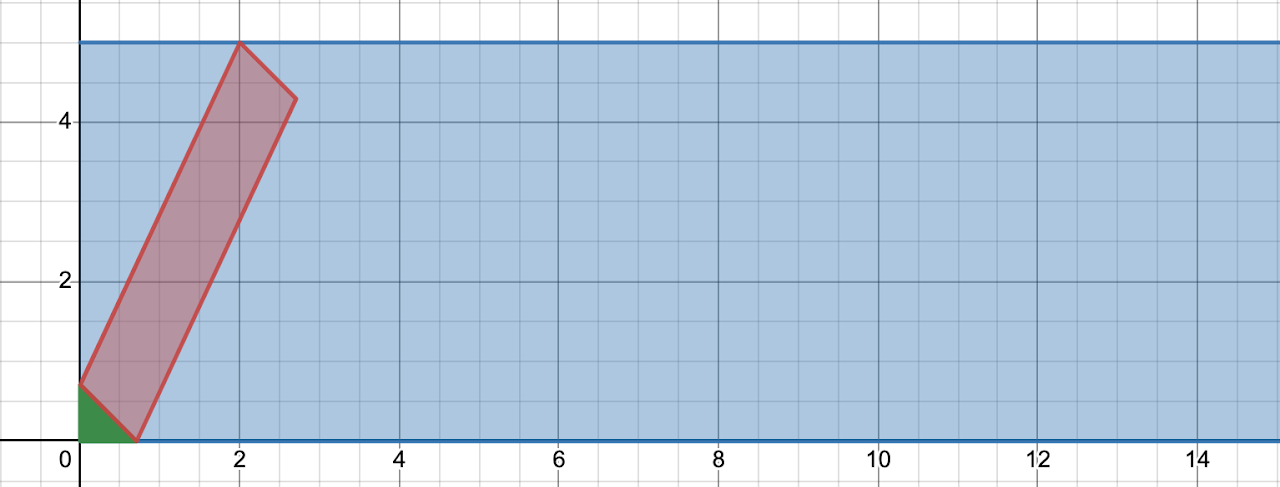
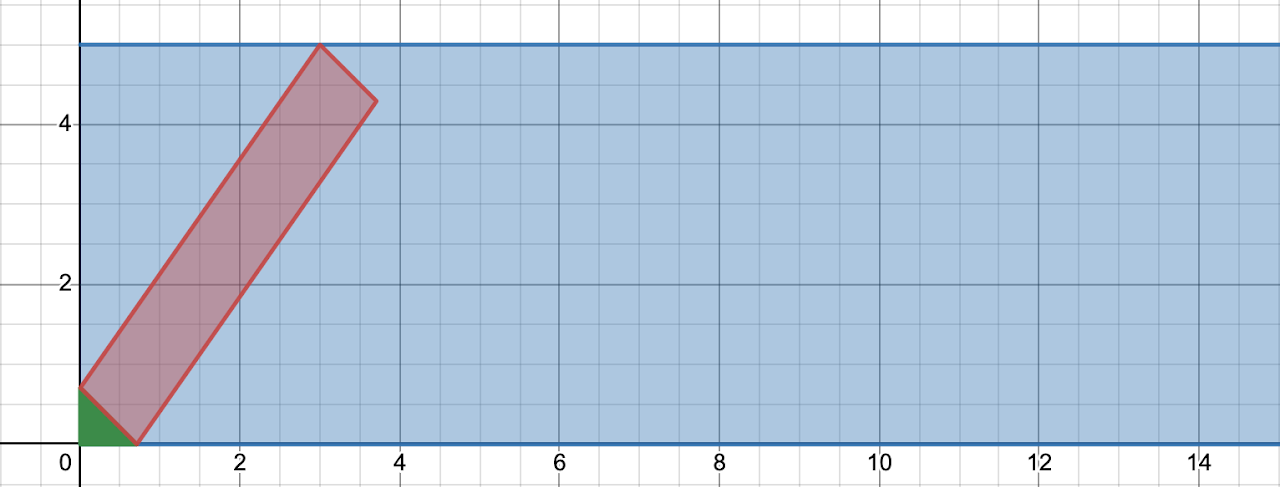
These are all parallelograms with the same base (the windshield itself). The areas might look the same, but the height is different. Another way to show that the areas are different is to consider the extreme case: going way too fast relative to the rain…

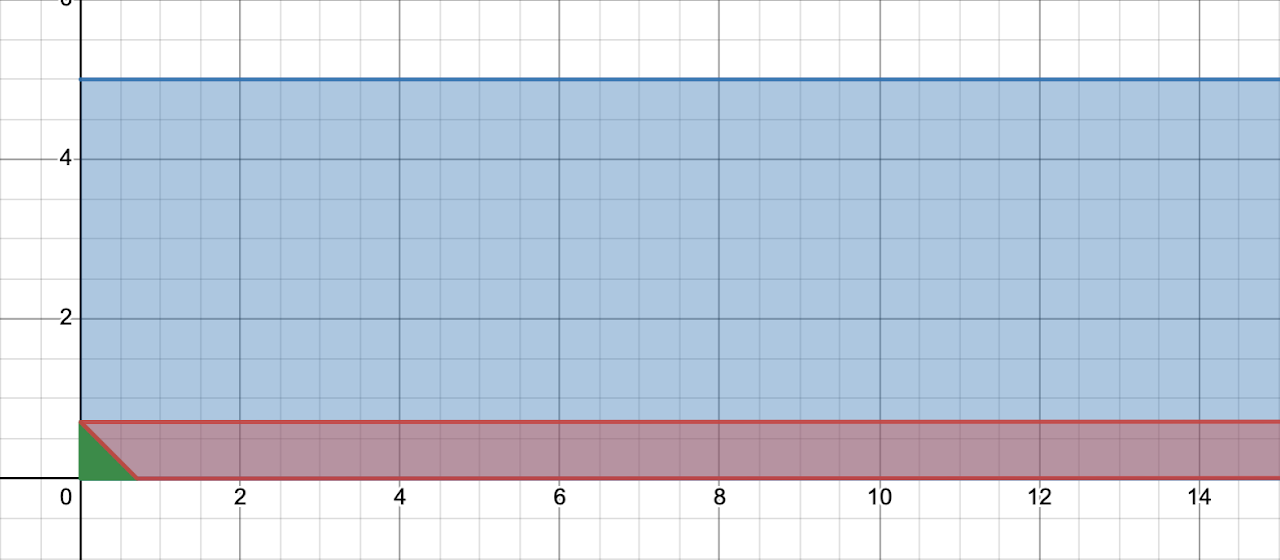
In this case, the area is almost just a rectangle with two negligible triangles on the sides. It takes a really long time for the rectangle to finish slanting upwards, and therefore, the area is also extremely large.

So having different speeds does have an effect on the amount of rain that gets on your windshield, but please don’t drive at 11176940.3652 MPH(approximately the speed of light) just to catch rain.

There is an exception to the differing speeds catching different amounts of rain: if your windshield is facing vertically, then the height of the parallelogram stays the same. This does create another question which is, “What is the optimal angle to catch the most rain for any combination of speed and rain?” Maybe you’re trying to cool your windshield down after driving at near the speed of light. (Not going to work)

Slight correction: instead of it saying, “either or probably”, it should say, “this and probably this too”

Now, think of this problem with the car as a reference point rather than the ground. The rain is now coming towards your windshield, with the car not moving. If we rotate this so that the windshield is facing directly up, it makes everything clearer. Unfortunately, rotation in Desmos is hard, so you have to imagine this.

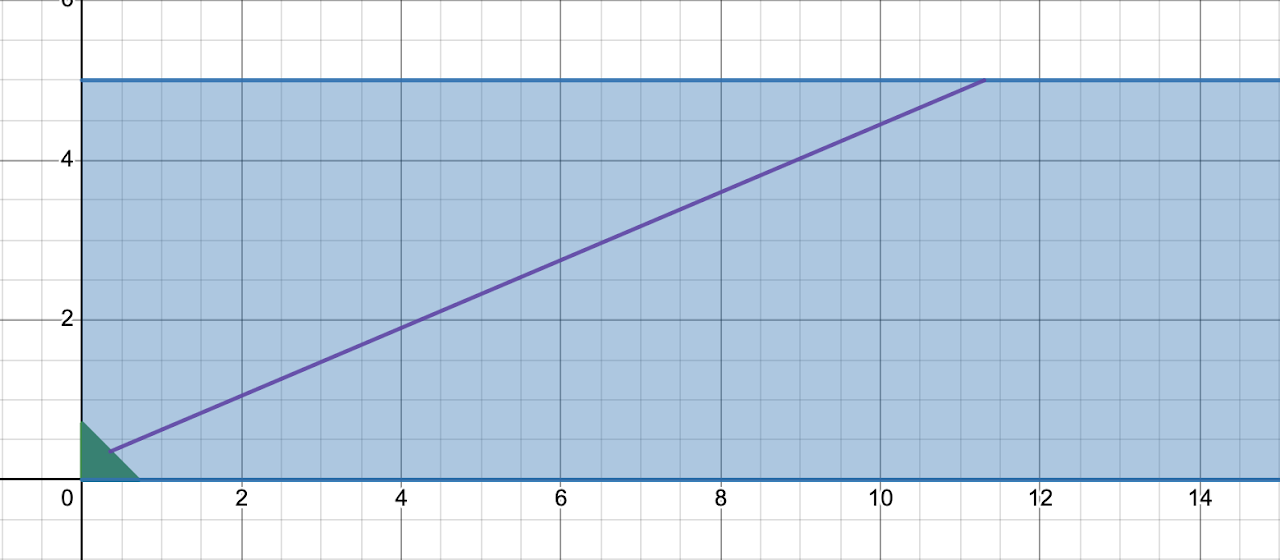
If the rain is at a slope of rainspeed/carspeed, the way the windshield is going to catch the most rain is to be perpendicular to it, since it is going to appear widest to the rain at that angle. Or, the windshield should be at the angle of tan(carspeed/rainspeed).